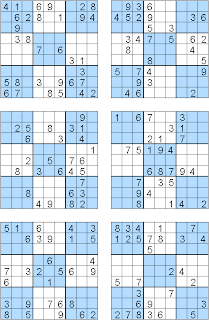
3rd batch of free printable sudoku puzzles - 60 Easy Sudoku Puzzles
Download link:-
http://rapidshare.com/files/132544070/Suduko3easy.pdf
http://www.mediafire.com/?xkxnn92idxt
Printable Sudoku Puzzle #2
Posted by
John
at
8:04 PM
|
Labels:
Easy difficulty,
hard difficulty,
Moderate difficulty,
printable sudoku puzzles
Second batch will include 36 easy, moderate and hard Sudoku puzzles. Enjoy!
Click on either of the links below to download this free printable sudoku puzzles.
http://rapidshare.com/files/125985475/Suduko2.pdf
http://www.mediafire.com/?xiegyxgmeny
Click on either of the links below to download this free printable sudoku puzzles.
http://rapidshare.com/files/125985475/Suduko2.pdf
http://www.mediafire.com/?xiegyxgmeny
Free Printable Sudoku #1
Posted by
John
at
8:14 PM
|
Labels:
Easy difficulty,
hard difficulty,
Moderate difficulty,
printable sudoku puzzles
This first batch of free printable sudoku puzzles will include 36 easy sudoku puzzles, 36 moderate sudoku puzzles and 48 hard sudoku puzzles.
Click on the link to download (2 mirrors):-
http://www.mediafire.com/?cjwpnhdnnv1
http://rapidshare.com/files/125531439/Suduko1.pdf
Enjoy!
Click on the link to download (2 mirrors):-
http://www.mediafire.com/?cjwpnhdnnv1
http://rapidshare.com/files/125531439/Suduko1.pdf
Enjoy!
ECOURSE PART 5: ELIMINATE THE EXTRANEOUS
We have looked at the basic number finding strategies, but what if these are just not up to the job? Until now we have been causally penciling in possible numbers, but there are many puzzles that will require you to be totally methodical in order to seek out and eliminate extraneous numbers.
If you have come to a point where obvious clues have dried up, before moving into unknown territory and beginning bifurcation (more on that later), you should ensure that you have actually found all the numbers that you can. The first step towards achieving this is to pencil in all possible numbers in each square. It takes less time than you would think to rattle off “can 1 go”, “can 2 go”, “can 3 go” while checking for these numbers in the cell’s region, row, and column.
It never hurts to repeat the one basic tenet of the Sudoku puzzle: if something is true for one element then it has to be true for the other two associated elements. Let’s look back to something that we looked at earlier: twins. When you discovering the rule about “twins” the grid wasn’t so crowded as it is in section of the Sudoku grid below.
This concludes our 5 part ecourse on "Sudoku Puzzle Secrets!"
If you have come to a point where obvious clues have dried up, before moving into unknown territory and beginning bifurcation (more on that later), you should ensure that you have actually found all the numbers that you can. The first step towards achieving this is to pencil in all possible numbers in each square. It takes less time than you would think to rattle off “can 1 go”, “can 2 go”, “can 3 go” while checking for these numbers in the cell’s region, row, and column.
It never hurts to repeat the one basic tenet of the Sudoku puzzle: if something is true for one element then it has to be true for the other two associated elements. Let’s look back to something that we looked at earlier: twins. When you discovering the rule about “twins” the grid wasn’t so crowded as it is in section of the Sudoku grid below.
This concludes our 5 part ecourse on "Sudoku Puzzle Secrets!"
ECOURSE PART 4: SEARCHING FOR THE LONE NUMBER
No matter what level of puzzle you are attempting to solve there are a few strategies that will allow you to get to a solution more quickly. The key strategy is to look for the lone number. In the following example, all the options for region 5 have been penciled in. At first there appear to be three places for the number 1 to go, but look between the 8 and the 3. There is a lone number 1.
It was not otherwise obvious that the only cell for the number 1 was row 6, column 5, as there is no number 1 in the immediate vicinity. Checking the adjacent regions and relevant row and column would not provide an immediate answer either – but no other number can go in that region.
While the example uses pencil marks to illustrate the rule, more experienced solvers are quite capable of doing this in their head. Remember that this principle is true for regions, rows, and columns: If there is only one place for a number to go, then it is true for that region, and also the row and column it is in. You can eliminate all the other pencilled 1’s in the region, row, and column.
Twins
Why limit yourself to one when sometimes two can do the job? In Sudoku you can easily become blind to the obvious. You might look at a region and think that there is no way of proving a number because it could go in more than one cell, but there are times when the answer is staring you right in the face. Sometimes the more obvious ways to find a solution is by looking at the obvious. Some solvers start by taking a few minutes to understand where the “givens” in the puzzle are laid out before they start to take any sort of solving action. This gives them a good feel for how easy or hard the puzzle is going to be so that they can apply certain strategies to their solving technique.
Next time we'll be discussing alittle about "Eliminate the extraneous".
It was not otherwise obvious that the only cell for the number 1 was row 6, column 5, as there is no number 1 in the immediate vicinity. Checking the adjacent regions and relevant row and column would not provide an immediate answer either – but no other number can go in that region.
While the example uses pencil marks to illustrate the rule, more experienced solvers are quite capable of doing this in their head. Remember that this principle is true for regions, rows, and columns: If there is only one place for a number to go, then it is true for that region, and also the row and column it is in. You can eliminate all the other pencilled 1’s in the region, row, and column.
Twins
Why limit yourself to one when sometimes two can do the job? In Sudoku you can easily become blind to the obvious. You might look at a region and think that there is no way of proving a number because it could go in more than one cell, but there are times when the answer is staring you right in the face. Sometimes the more obvious ways to find a solution is by looking at the obvious. Some solvers start by taking a few minutes to understand where the “givens” in the puzzle are laid out before they start to take any sort of solving action. This gives them a good feel for how easy or hard the puzzle is going to be so that they can apply certain strategies to their solving technique.
Next time we'll be discussing alittle about "Eliminate the extraneous".
ECOURSE PART 3: BEGINNING THE CHALLENGE
Below is an unsolved Sudoku puzzle. It consists of a 9 x 9 grid that has been subdivided into 9 smaller grids of 3 x 3 squares. Each puzzle has a logical and a unique solution. To solve the puzzle, each row, column, and box must contain each of the numbers 1 to 9. Throughout this guide the entire puzzle will be referred to the “grid”, a small 3 x 3 grid as a “region”, and the square that contains the number as the “cell”.
Rows and columns are referred to with row number first, followed by the column number:
4,5 is row 4, column 5
2,8 is row 2, column 8
Boxes are numbered 1 – 9 in reading order: 123 456 789
Guessing
Try not to guess. Until you have progressed to the touch and diabolical puzzles, guessing is not only totally unnecessary, but will lead you up paths that can make the puzzle virtually unsolvable. Simple logic is all that is required for gentle and moderate puzzles. Most puzzles that are rated easy to hard will require some sort of analysis.
Starting the Game
To solve Sudoku puzzles you will need to use logic. You need to ask yourself questions like “if a 1 is in this cell, will it go in this column?” or “if a 9 is already in this row, can a 9 go in this cell?” To make a start, look at each of the regions in the grid below and see which cells are empty, at the same time checking that cell’s column and row for a missing number. In this example, look at region 9. There is no 8 in the region, but there is an 8 in column 7 and in column 8. The only place for an 8 is in column 9, and in this box the only cell available is in row 9. So put an 8 in that cell. Once you have done this you have solved your first number.
Next time we'll be discussing alittle about "Searching for the lone number".
Rows and columns are referred to with row number first, followed by the column number:
4,5 is row 4, column 5
2,8 is row 2, column 8
Boxes are numbered 1 – 9 in reading order: 123 456 789
Guessing
Try not to guess. Until you have progressed to the touch and diabolical puzzles, guessing is not only totally unnecessary, but will lead you up paths that can make the puzzle virtually unsolvable. Simple logic is all that is required for gentle and moderate puzzles. Most puzzles that are rated easy to hard will require some sort of analysis.
Starting the Game
To solve Sudoku puzzles you will need to use logic. You need to ask yourself questions like “if a 1 is in this cell, will it go in this column?” or “if a 9 is already in this row, can a 9 go in this cell?” To make a start, look at each of the regions in the grid below and see which cells are empty, at the same time checking that cell’s column and row for a missing number. In this example, look at region 9. There is no 8 in the region, but there is an 8 in column 7 and in column 8. The only place for an 8 is in column 9, and in this box the only cell available is in row 9. So put an 8 in that cell. Once you have done this you have solved your first number.
Next time we'll be discussing alittle about "Searching for the lone number".
ECOURSE PART 2: SOLUTION METHOD-SCANNING
Scanning is one way that you can solve a Sudoku puzzle. When you first look at that puzzle you should scan it at least once and again a few times while you are trying to arrive at the solution. Take some time to analyze the puzzle as you are working it since scanning can help you to quickly pick up on a working in one or two needed numbers.
There are two basic techniques when it comes to scanning: cross-hatching and counting. You can use both of these methods alternately.
You won’t be able to scan the puzzle any further when you run out of numbers to put into cells. After this you will need to start working the puzzle from a logical stand point. Some people find that it helps to mark possible numbers in the cells. You can do this using either subscripts or dots:
There are two basic techniques when it comes to scanning: cross-hatching and counting. You can use both of these methods alternately.
You won’t be able to scan the puzzle any further when you run out of numbers to put into cells. After this you will need to start working the puzzle from a logical stand point. Some people find that it helps to mark possible numbers in the cells. You can do this using either subscripts or dots:
- Subscript marking: Use subscript to mark possible number into the cells. The one disadvantage to this is that many puzzles, such as those found in newspapers, are often too small to allow you to write in the cells. Consider making a larger copy of the puzzle so that you can read it easier or use a pencil that is very sharp so that you can write fine lines.
- Dot marking: Dot marking involves using a pattern of dots. A dot in the top left will indicate a one and dot in the bottom right will indicate a 9. The advantage of using the dot notation is that you can easily use it on the original puzzle. You will have to make sure that you don’t make a mistake with the dots or you will be led into confusion and it may not be easy to erase dots without creating more confusion.
ECOURSE PART 1: THE MATH BEHIND SUDOKU
The Sudoku puzzle is unlike most puzzles in that it is based on mathematical structure and requires some level of logic in order to be solved. The main basis behind solving Sudoku is called “NP-complete” because it is solved on n2 x n2 grids of n x n cells. It is this concept that makes Sudoku so difficult to solve. When you put cells on grids and throw in a few “givens” it takes some determining finite power to solve the puzzle correctly.
Sudoku has what is known as a “game tree”. The game tree of this puzzle game is quite large and, when there is only one solution to be found, makes solving it fast an unfeasible plan. There are, however, tips that you can use to solve Sudoku as fast as possible.
Perhaps an easy way of describing the solution of a Sudoku puzzle is to call it a “graph coloring problem”. The basic goal of the puzzle is to build, in its standard form of 9 x 9, a coloring grid. The entirety of the graph is composed of 81 vertices, with one vertex for every cell on the grid. Each of the vertices can be named with pairs that are ordered and where “x” and “y” are integers anywhere from one to nine. This means that two separate vertices are names and are connected by an edge if, and only if the edges match. The Sukoku puzzle is eventually solved by assigning an integer, from one to nine, to each of the vertices in a way where the vertices connected by an edge don't have the same integer assigned to them.
A Latin Square
The solution of the Sudoku grid is much like a Latin square. There are, however, less solution grids for Sudoku, than there are Latin squares. This is because Sudoku has the additional problem of multiple regions. Still, there are endless solution grids for the Sudoku puzzle. In 2005 Bertram Felgenhauer calculated the number to be about 6,670,903,752,021,072,936,960. He arrived at this number using logical computations. The analysis of the number of solution grids was further simplified by Frazer Jarvis and Ed Russell. It has not yet been calculated how many solution grids there are for the 16 x 16 Sudoku puzzle.
Next time we'll be discussing alittle about "Solution methods-scanning".
Sudoku has what is known as a “game tree”. The game tree of this puzzle game is quite large and, when there is only one solution to be found, makes solving it fast an unfeasible plan. There are, however, tips that you can use to solve Sudoku as fast as possible.
Perhaps an easy way of describing the solution of a Sudoku puzzle is to call it a “graph coloring problem”. The basic goal of the puzzle is to build, in its standard form of 9 x 9, a coloring grid. The entirety of the graph is composed of 81 vertices, with one vertex for every cell on the grid. Each of the vertices can be named with pairs that are ordered and where “x” and “y” are integers anywhere from one to nine. This means that two separate vertices are names and are connected by an edge if, and only if the edges match. The Sukoku puzzle is eventually solved by assigning an integer, from one to nine, to each of the vertices in a way where the vertices connected by an edge don't have the same integer assigned to them.
A Latin Square
The solution of the Sudoku grid is much like a Latin square. There are, however, less solution grids for Sudoku, than there are Latin squares. This is because Sudoku has the additional problem of multiple regions. Still, there are endless solution grids for the Sudoku puzzle. In 2005 Bertram Felgenhauer calculated the number to be about 6,670,903,752,021,072,936,960. He arrived at this number using logical computations. The analysis of the number of solution grids was further simplified by Frazer Jarvis and Ed Russell. It has not yet been calculated how many solution grids there are for the 16 x 16 Sudoku puzzle.
Next time we'll be discussing alittle about "Solution methods-scanning".
Subscribe to:
Comments (Atom)